Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

Number of solutions $vertical line 1 divided by left parenthesis vertical line x vertical line minus 1 right parenthesis vertical line equals x plus sin invisible function application x$

1
2
3
4

The correct answer is: 1

Related Questions to study

A tangent galvanometer has a coil of 25 turns and radius of 15 cm. The horizontal component of the earth’s magnetic field is 3 ´ 10^–5 T. The current required to produce a deflection of 45^o in it, is

A tangent galvanometer has a coil of 25 turns and radius of 15 cm. The horizontal component of the earth’s magnetic field is 3 ´ 10^–5 T. The current required to produce a deflection of 45^o in it, is

Physics-General

When $square root of 3$ ampere current is passed in a tangent galvanometer, there is a deflection of 30° in it. The deflection obtained when 3 amperes current is passed, is

When $square root of 3$ ampere current is passed in a tangent galvanometer, there is a deflection of 30° in it. The deflection obtained when 3 amperes current is passed, is

Physics-General

The time period of a bar magnet suspended horizontally in the earth's magnetic field and allowed to oscillate

The time period of a bar magnet suspended horizontally in the earth's magnetic field and allowed to oscillate

Physics-General

parallel

Time period for a magnet is T. If it is divided in four equal parts along its axis and perpendicular to its axis as shown then time period for each part will be

Time period for a magnet is T. If it is divided in four equal parts along its axis and perpendicular to its axis as shown then time period for each part will be

Physics-General

At a certain place a magnet makes 30 oscillations per minute. At another place where the magnetic field is double, its time period will be

At a certain place a magnet makes 30 oscillations per minute. At another place where the magnetic field is double, its time period will be

Physics-General

At which place, earth's magnetism become horizontal

At which place, earth's magnetism become horizontal

Physics-General

parallel

At a certain place the horizontal component of the earth’s magnetic field is B₀ and the angle of dip is 45^o. The total intensity of the field at that place will be

At a certain place the horizontal component of the earth’s magnetic field is B₀ and the angle of dip is 45^o. The total intensity of the field at that place will be

Physics-General

At a certain place, the horizontal component $B subscript 0 end subscript$ and the vertical component $V subscript 0 end subscript$ of the earth's magnetic field are equal in magnitude. The total intensity at the place will be

At a certain place, the horizontal component $B subscript 0 end subscript$ and the vertical component $V subscript 0 end subscript$ of the earth's magnetic field are equal in magnitude. The total intensity at the place will be

Physics-General

Lines which represent places of constant angle of dip are called

Lines which represent places of constant angle of dip are called

Physics-General

parallel

At a place, the horizontal and vertical intensities of earth's magnetic field is 0.30 Gauss and 0.173 Gauss respectively. The angle of dip at this place is

At a place, the horizontal and vertical intensities of earth's magnetic field is 0.30 Gauss and 0.173 Gauss respectively. The angle of dip at this place is

Physics-General

The angle of dip is the angle

The angle of dip is the angle

Physics-General

If the normal at the points P_i (x_i, y_i), i = 1 to 4 on the hyperbola xy = c² are concurrent at the point Q(h, k), then $fraction numerator open parentheses x subscript 1 end subscript plus x subscript 2 end subscript plus x subscript 3 end subscript plus x subscript 4 end subscript close parentheses open parentheses y subscript 1 end subscript plus y subscript 2 end subscript plus y subscript 3 end subscript plus y subscript 4 end subscript close parentheses over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction$ is equal to

If the normal at the points P_i (x_i, y_i), i = 1 to 4 on the hyperbola xy = c² are concurrent at the point Q(h, k), then $fraction numerator open parentheses x subscript 1 end subscript plus x subscript 2 end subscript plus x subscript 3 end subscript plus x subscript 4 end subscript close parentheses open parentheses y subscript 1 end subscript plus y subscript 2 end subscript plus y subscript 3 end subscript plus y subscript 4 end subscript close parentheses over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction$ is equal to

parallel

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

According to Huckel’s rule a compound is said to be aromatic if it contains

According to Huckel’s rule a compound is said to be aromatic if it contains

Chemistry-General

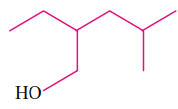structure is

structure is

Chemistry-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.